人工智能
神经网络简单介绍
遍地开花的 Attention,你真的懂吗?
注意力机制到底在做什么,Q/K/V怎么来的?一文读懂Attention注意力机制
FlashAttention图解(如何加速Attention)
FlashAttention2详解(性能比FlashAttention提升200%)
【Attention(4)】【QKV的自注意力机制】 主要思路(笔记)
-
+
首页
神经网络简单介绍
刚刚入门神经网络,往往会对众多的神经网络架构感到困惑,神经网络看起来复杂多样,但是这么多架构无非也就是三类,前馈神经网络,循环网络,对称连接网络,本文将介绍四种常见的神经网络,分别是 CNN,RNN,DBN,GAN。通过这四种基本的神经网络架构,我们来对神经网络进行一定的了解。 什么是神经网络 ------- **神经网络是机器学习中的一种模型,是一种模仿动物神经网络行为特征,进行分布式并行信息处理的算法数学模型。**这种网络依靠系统的复杂程度,通过调整内部大量节点之间相互连接的关系,从而达到处理信息的目的。 一般来说,神经网络的架构可以分为三类: **前馈神经网络:** 这是实际应用中最常见的神经网络类型。**第一层是输入,最后一层是输出。如果有多个隐藏层,我们称之为 “深度” 神经网络。他们计算出一系列改变样本相似性的变换。**各层神经元的活动是前一层活动的非线性函数。 **循环网络:** **循环网络在他们的连接图中定向了循环,这意味着你可以按照箭头回到你开始的地方。他们可以有复杂的动态,使其很难训练。**他们更具有生物真实性。 **循环网络的目的使用来处理序列数据。在传统的神经网络模型中,是从输入层到隐含层再到输出层,层与层之间是全连接的,每层之间的节点是无连接的。**但是这种普通的神经网络对于很多问题却无能无力。例如,你要预测句子的下一个单词是什么,一般需要用到前面的单词,因为一个句子中前后单词并不是独立的。 循环神经网路,即一个序列当前的输出与前面的输出也有关。具体的表现形式为网络会对前面的信息进行记忆并应用于当前输出的计算中,即隐藏层之间的节点不再无连接而是有连接的,并且隐藏层的输入不仅包括输入层的输出还包括上一时刻隐藏层的输出。 **对称连接网络:** 对称连接网络有点像循环网络,但是单元之间的连接是对称的(它们在两个方向上权重相同)。比起循环网络,对称连接网络更容易分析。这个网络中有更多的限制,因为它们遵守能量函数定律。没有隐藏单元的对称连接网络被称为 “Hopfield 网络”。有隐藏单元的对称连接的网络被称为玻尔兹曼机。 感知机 --- 其实之前的帖子讲过一些关于感知机的内容,这里再复述一下。 首先还是这张图 这是一个 M-P 神经元  神经元 **一个神经元有 n 个输入,每一个输入对应一个权值 w,神经元内会对输入与权重做乘法后求和,求和的结果与偏置做差,最终将结果放入激活函数中,由激活函数给出最后的输出,输出往往是二进制的,0 状态代表抑制,1 状态代表激活。**  感知机的输出 感知机可以分为单层感知机,多层感知机。 我们这里主要讨论的是单层感知机。 而感知机由两层神经网络组成,输入层接收外界输入信号后传递给输出层,输出层是 M-P 神经元,  **感知机** 可以把感知机看作是 n 维实例空间中的超平面决策面,对于超平面一侧的样本,感知器输出 1,对于另一侧的实例输出 0,这个决策超平面方程是 w⋅x=0。 **那些可以被某一个超平面分割的正反样例集合称为线性可分 (linearly separable) 样例集合,它们就可以使用图中的感知机表示。** - **超平面决策面** - **超平面决策面是机器学习中一种常用的分类方法,它可以将样本空间划分为两个不同的区域,用于将具有不同类别的样本分开。**超平面是一个(d-1)维的线性子空间,其中d是样本特征的维数。在二分类问题中,超平面将样本空间划分为正例和反例两个区域,使得正例尽可能靠近一个区域,反例尽可能靠近另一个区域。 - **维数** - **维数是指在一个向量空间中所需要的线性无关的基向量的个数。**在数学和几何中,维数是描述向量空间或一个对象所占用的空间的量度。 - **基向量** - 基向量是向量空间中的一组线性无关的向量,它们可以通过线性组合来表示该向量空间中的任意向量。基向量是向量空间的一个基础,它可以用来描述向量空间的维度和表示向量空间中的向量。 - 维数可以用于描述多种对象,如点、线、平面、立体等。对于一个向量空间,维数是指空间中的向量所包含的独立维度的数量。**例如,二维平面上的向量空间具有两个维度,即平面上的任意向量可以由两个基向量线性组合而成。类似地,三维空间中的向量空间具有三个维度,四维空间具有四个维度,以此类推。** - **在机器学习和数据分析中,维数也常用于描述数据集的特征数量。**例如,在一个包含100个样本和10个特征的数据集中,每个样本可以表示为一个10维的向量。这个数据集的特征维数为10。 - 维数的概念在很多领域都有广泛的应用,包括线性代数、几何学、数据分析、机器学习等。理解维数对于理解和描述向量空间、数据集以及相关算法和模型的特征具有重要意义。 - 超平面决策面的方程可以表示为: - w^T * x + b = 0 - 其中,w是一个d维的权重向量,x是一个d维的特征向量,b是一个常数偏置项。超平面将样本空间划分为两个区域:w^T * x + b > 0表示正例区域,w^T * x + b < 0表示反例区域。样本点x在超平面上时,w^T * x + b = 0。 - **超平面决策面的选择是为了最大化分类的间隔,即使得正例和反例之间的距离最大化。**在实际应用中,通常使用支持向量机(SVM)算法来学习超平面决策面,以实现更好的分类效果。 与、或、非问题都是线性可分的问题,使用一个有两输入的感知机能容易地表示,而异或并不是一个线性可分的问题,所以使用单层感知机是不行的,这时候就要使用多层感知机来解决疑惑问题了。 如果我们要训练一个感知机,应该怎么办呢? **我们会从随机的权值开始,反复地应用这个感知机到每个训练样例,只要它误分类样例就修改感知机的权值。重复这个过程,直到感知机正确分类所有的样例。**每一步根据感知机训练法则来修改权值,也就是修改与输入 xi 对应的权 wi,法则如下:  image **这里 t 是当前训练样例的目标输出,o 是感知机的输出,η 是一个正的常数称为学习速率。学习速率的作用是缓和每一步调整权的程度,它通常被设为一个小的数值(例如 0.1),而且有时会使其随着权调整次数的增加而衰减。*** 多层感知机,或者说是多层神经网络无非就是在输入层与输出层之间加了多个隐藏层而已,后续的 CNN,DBN 等神经网络只不过是将重新设计了每一层的类型。感知机可以说是神经网络的基础,后续更为复杂的神经网络都离不开最简单的感知机的模型, 卷积神经网络 CNN ---------- 谈到机器学习,我们往往还会跟上一个词语,叫做模式识别,但是真实环境中的模式识别往往会出现各种问题。比如: 图像分割:真实场景中总是掺杂着其它物体。很难判断哪些部分属于同一个对象。对象的某些部分可以隐藏在其他对象的后面。 物体光照:像素的强度被光照强烈影响。 图像变形:物体可以以各种非仿射方式变形。例如,手写也可以有一个大的圆圈或只是一个尖头。 情景支持:物体所属类别通常由它们的使用方式来定义。例如,椅子是为了让人们坐在上面而设计的,因此它们具有各种各样的物理形状。 **卷积神经网络与普通神经网络的区别在于,卷积神经网络包含了一个由卷积层和子采样层构成的特征抽取器。在卷积神经网络的卷积层中,一个神经元只与部分邻层神经元连接。**在 CNN 的一个卷积层中,通常包含若干个特征平面 (featureMap),每个特征平面由一些矩形排列的的神经元组成,同一特征平面的神经元共享权值,这里共享的权值就是卷积核。卷积核一般以随机小数矩阵的形式初始化,在网络的训练过程中卷积核将学习得到合理的权值。共享权值(卷积核)带来的直接好处是减少网络各层之间的连接,同时又降低了过拟合的风险。**子采样也叫做池化(pooling),通常有均值子采样(mean pooling)和最大值子采样(max pooling)两种形式。子采样可以看作一种特殊的卷积过程。卷积和子采样大大简化了模型复杂度,减少了模型的参数。** **卷积神经网络由三部分构成。第一部分是输入层。第二部分由 n 个卷积层和池化层的组合组成。第三部分由一个全连结的多层感知机分类器构成。** 这里举 AlexNet 为例:  image · 输入:224×224 大小的图片,3 通道 · 第一层卷积:11×11 大小的卷积核 96 个,每个 GPU 上 48 个。 · 第一层 max-pooling:2×2 的核。 · 第二层卷积:5×5 卷积核 256 个,每个 GPU 上 128 个。 · 第二层 max-pooling:2×2 的核。 · 第三层卷积:与上一层是全连接,3*3 的卷积核 384 个。分到两个 GPU 上个 192 个。 · 第四层卷积:3×3 的卷积核 384 个,两个 GPU 各 192 个。该层与上一层连接没有经过 pooling 层。 · 第五层卷积:3×3 的卷积核 256 个,两个 GPU 上个 128 个。 · 第五层 max-pooling:2×2 的核。 · 第一层全连接:4096 维,将第五层 max-pooling 的输出连接成为一个一维向量,作为该层的输入。 · 第二层全连接:4096 维 ·Softmax 层:输出为 1000,输出的每一维都是图片属于该类别的概率。 卷积神经网络在模式识别领域有着重要应用,当然这里只是对卷积神经网络做了最简单的讲解,卷积神经网络中仍然有很多知识,比如局部感受野,权值共享,多卷积核等内容,后续有机会再进行讲解。 循环神经网络(递归神经网络) RNN ------------------ **传统的神经网络对于很多问题难以处理,比如你要预测句子的下一个单词是什么,一般需要用到前面的单词,因为一个句子中前后单词并不是独立的。**RNN 之所以称为循环神经网路,即一个序列当前的输出与前面的输出也有关。具体的表现形式为网络会对前面的信息进行记忆并应用于当前输出的计算中,即隐藏层之间的节点不再无连接而是有连接的,并且隐藏层的输入不仅包括输入层的输出还包括上一时刻隐藏层的输出。**理论上,RNN 能够对任何长度的序列数据进行处理。 这是一个简单的 RNN 的结构,可以看到隐藏层自己是可以跟自己进行连接的。**  RNN 那么 RNN 为什么隐藏层能够看到上一刻的隐藏层的输出呢,其实我们把这个网络展开来开就很清晰了。  image **这个网络在 t 时刻接收到输入 Xt 之后,隐藏层的值是 St, 输出值是 Ot, 关键一点是,St的值不仅仅取决于 Xt,还取决于 St-1。**  image 式 1 是输出层的计算公式,输出层是一个全连接层,也就是它的每个节点都和隐藏层的每个节点相连。V 是输出层的权重矩阵,g 是激活函数。 式 2 是隐藏层的计算公式,它是循环层。U 是输入 x 的权重矩阵,W 是上一次的值 St-1 作为这一次的输入的权重矩阵,f 是激活函数。 - **全连接层** - **全连接层(Fully Connected Layer),也称为密集连接层或全连接层,是深度学习神经网络中的一种常见层类型。全连接层的每个神经元都与上一层的所有神经元相连,因此它的每个输入都会对所有输出产生影响。** - **在全连接层中,每个神经元都有一个权重(weight)与其连接的上一层神经元的输出相关联。通过将上一层的所有神经元的输出与相应的权重相乘并求和,然后通过激活函数进行非线性变换,可以得到该层的输出。这个过程可以表示为:** - **y = f(Wx + b)** - **其中,W是权重矩阵,x是上一层的输出向量,b是偏置向量,f()是激活函数,y是当前层的输出向量。** - 全连接层的作用是从上一层的输出中提取更高级别的特征,并将这些特征传递给下一层进行进一步处理。全连接层通常用于神经网络的最后几层,用于分类、回归等任务。在深度学习中,全连接层往往与其他类型的层(如卷积层、池化层等)交替使用,形成一个完整的神经网络模型。 从上面的公式我们可以看出,循环层和全连接层的区别就是循环层多了一个权重矩阵 W。 如果反复把式 2 带入到式 1,我们将得到:  image 从上面可以看出,**循环神经网络的输出值,是受前面历次输入值 Xt、Xt-1、Xt-2、X-3、X-4... 影响的**,这就是为什么循环神经网络可以往前看任意多个输入值的原因。 深度信念网络 DBN ---------- 在讲 DBN 之前,我们需要对 DBN 的基本组成单位有一定的了解,那就是 RBM,受限玻尔兹曼机。 首先什么是玻尔兹曼机? 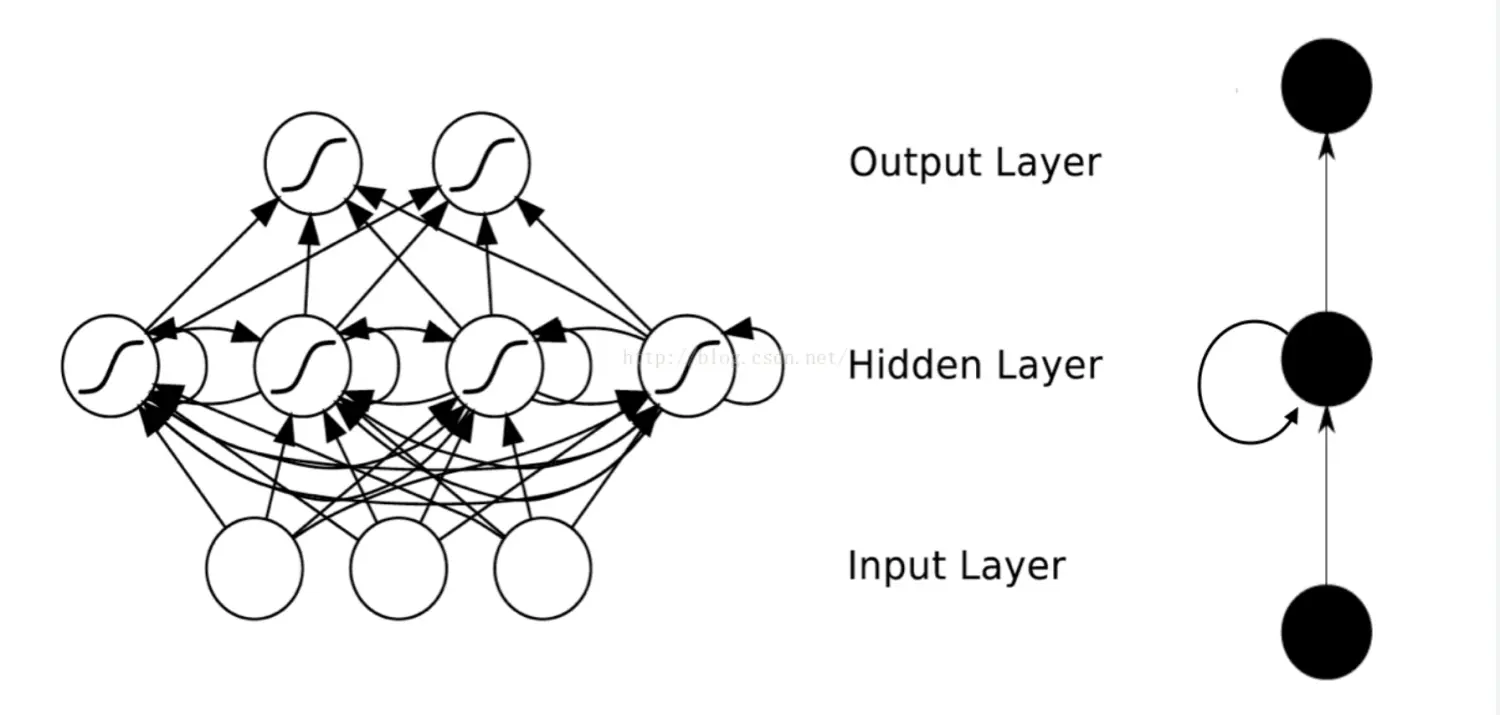 如图所示为一个玻尔兹曼机,其蓝色节点为隐层,白色节点为输入层。 玻尔兹曼机和递归神经网络相比,区别体现在以下几点: 1、递归神经网络本质是学习一个函数,因此有输入和输出层的概念,而玻尔兹曼机的用处在于学习一组数据的 “内在表示”,因此其没有输出层的概念。 2、递归神经网络各节点链接为有向环,而玻尔兹曼机各节点连接成无向完全图。 而受限玻尔兹曼机是什么呢? 最简单的来说就是加入了限制,这个限制就是将完全图变成了二分图。即由一个显层和一个隐层构成,显层与隐层的神经元之间为双向全连接。  RBM h 表示隐藏层,v 表示显层 **在 RBM 中,任意两个相连的神经元之间有一个权值 w 表示其连接强度,每个神经元自身有一个偏置系数 b(对显层神经元)和 c(对隐层神经元)来表示其自身权重。** 具体的公式推导在这里就不展示了 DBN 是一个概率生成模型,与传统的判别模型的神经网络相对,生成模型是建立一个观察数据和标签之间的联合分布,对 P(Observation|Label) 和 P(Label|Observation) 都做了评估,而判别模型仅仅而已评估了后者,也就是 P(Label|Observation)。 DBN 由多个限制玻尔兹曼机(Restricted Boltzmann Machines)层组成,一个典型的神经网络类型如图所示。这些网络被 “限制” 为一个可视层和一个隐层,层间存在连接,但层内的单元间不存在连接。隐层单元被训练去捕捉在可视层表现出来的高阶数据的相关性。 - **隐层** - **隐层(Hidden Layer)是深度学习神经网络中的一种层类型,位于输入层和输出层之间。与输入层和输出层不同,隐层的神经元既不是直接接收外部输入数据,也不是直接产生最终输出结果,而是通过学习和处理输入数据中的特征来进行信息变换。** - **隐层的作用是对输入数据进行非线性映射和特征提取,以便更好地表达和表示数据中的复杂关系。**通过通过一系列的权重和激活函数的计算,隐层可以将输入数据映射到更高维度的特征空间中,从而提取出更具有区分性的特征。 - **深度学习模型中的神经网络往往包含多个隐层,这也是为什么它被称为“深度”学习的原因。**每个隐层可以具有不同的神经元数量和激活函数,以适应不同的任务和数据特征。 - **隐层的设计和选择是深度学习模型设计中的重要考虑因素。**适当的隐层数量和神经元数量可以提高模型的表达能力和学习能力,但过多的隐层和神经元数量可能会导致过拟合的问题。  DBN 生成对抗网络 GAN ---------- 生成对抗网络其实在之前的帖子中做过讲解,这里在说明一下。 **生成对抗网络的目标在于生成,我们传统的网络结构往往都是判别模型,即判断一个样本的真实性。**而生成模型能够根据所提供的样本生成类似的新样本,注意这些样本是由计算机学习而来的。 **GAN 一般由两个网络组成,生成模型网络,判别模型网络。** **生成模型 G 捕捉样本数据的分布,用服从某一分布(均匀分布,高斯分布等)的噪声 z 生成一个类似真实训练数据的样本,追求效果是越像真实样本越好;判别模型 D 是一个二分类器,估计一个样本来自于训练数据(而非生成数据)的概率,如果样本来自于真实的训练数据,D 输出大概率,否则,D 输出小概率。** 举个例子:生成网络 G 好比假币制造团伙,专门制造假币,判别网络 D 好比警察,专门检测使用的货币是真币还是假币,G 的目标是想方设法生成和真币一样的货币,使得 D 判别不出来,D 的目标是想方设法检测出来 G 生成的假币。 传统的判别网络:  传统的判别网络 生成对抗网络:  生成对抗网络 **在训练的过程中固定一方,更新另一方的网络权重,交替迭代,在这个过程中,双方都极力优化自己的网络,从而形成竞争对抗,直到双方达到一个动态的平衡(纳什均衡),此时生成模型 G 恢复了训练数据的分布(造出了和真实数据一模一样的样本),判别模型再也判别不出来结果,准确率为 50%。** 下面展示一个 cDCGAN 的例子(前面帖子中写过的) 生成网络  生成网络 判别网络  判别网络 最终结果,使用 MNIST 作为初始样本,通过学习后生成的数字,可以看到学习的效果还是不错的。  生成网络 小结 -- 本文非常简单的介绍了四种神经网络的架构,CNN,RNN,DBN,GAN。当然也仅仅是简单的介绍,并没有深层次讲解其内涵。这四种神经网络的架构十分常见,应用也十分广泛。当然关于神经网络的知识,不可能几篇帖子就讲解完,这里知识讲解一些基础知识,帮助大家快速入(zhuang)门(bi)。后面的帖子将对深度自动编码器,Hopfield 网络长短期记忆网络(LSTM)进行讲解。
yg9538
2023年8月25日 20:41
转发文档
收藏文档
上一篇
下一篇
手机扫码
复制链接
手机扫一扫转发分享
复制链接
Markdown文件
Word文件
PDF文档
PDF文档(打印)
分享
链接
类型
密码
更新密码
有效期